ทำไมเราต้องเรียนแคลคูลัส +Clip (What is Calculus used for? | How to use calculus in real life )

ทำไมเราต้องเรียนแคลคูลัส

แคลคูลัสเป็นคณิตศาสตร์แขนงหนึ่งที่เด็กมหาวิทยาลัยที่เรียนด้านวิทยาศาสตร์ วิศวกรรมศาสตร์ จนถึง เศรษฐศาสตร์และด้านบัญชี ต้องพบเจอ หลายๆคนอาจเจ็บปวดไปกับการพยายามก้าวข้ามมันไปให้ได้(และหลายคนอาจพยายามอยู่หลายปี)

คำถามคือแล้วทำไมหลายคณะต้องเรียนวิชานี้
..................................................
จริงๆแล้ววิชาแคลคูลัสมีปรัชญาที่เรียบง่าย

คุณสมบัติของเส้นโค้งสักเส้นหนึ่งที่นักคณิตศาสตร์สนใจ
หลักๆแล้วมีอยู่สองอย่างคือ

1.ความชันของเส้นโค้ง (Slope)

2.พื้นที่ที่เส้นโค้งนั้นปิดล้อม

พื้นที่ปิดล้อมนั้นเข้าใจไม่ยาก แต่การจะเข้าใจความชันอาจต้องยกตัวอย่างเล็กน้อย

ลองนึกถึงสะพานข้ามแม่น้ำที่โค้งเหมือนรุ้งกินน้ำ

หากเราวางลูกฟุตบอลไว้กลางสะพานซึ่งเป็นตำแหน่งที่สูงจากตีนสะพานที่สุด ลูกฟุตบอลจะไม่กลิ้งไปไหน เพราะที่ตำแหน่งนั้นมีความชันเป็นศูนย์

แต่เมื่อวางลูกฟุตบอลที่ตำแหน่งอื่นๆของสะพาน ลูกฟุตบอลจะกลิ้งเพราะสะพานมีความชัน

ความชันที่แตกต่างกันจะส่งผลให้ลูกฟุตบอลกลิ้งด้วยอัตราที่เร่งเริ่มต้นที่แตกต่างกัน

คำถาม คือ เราจะรู้ได้อย่างไรว่าที่ตำแหน่งใดๆบนสะพานมีความชันเป็นเท่าใด และพื้นที่ใต้สะพานโค้งๆที่จากตำแหน่งหนึ่งถึงตำแหน่งหนึ่งมีค่าเท่าใด

ก่อนแคลคูลัสจะเกิดขึ้น

มีการพยายามศึกษาปริมาณต่างๆที่เกี่ยวข้องกับเส้นโค้งมาตั้งแต่สมัยกรีกโบราณแล้ว แต่วิธีการเหล่านั้นยุ่งยาก ช่วยหาคำตอบได้อย่างจำกัดรูปแบบและยังไม่มีกระบวนการแก้ปัญหาที่เป็นระบบ

แต่แคลคูลัสนั้นได้เข้ามาหาคำตอบเหล่านี้ได้อย่างง่ายดาย(ถ้าเราตั้งใจเรียน) โดย แคลคูลัสนั้นแบ่งออกเป็นสองส่วน คือ

1.ดิฟเฟอเรนเชียล แคลคูลัส (differential calculus) การคำนวณอัตราการเปลี่ยนแปลง หาความชันของกราฟ ฯลฯ
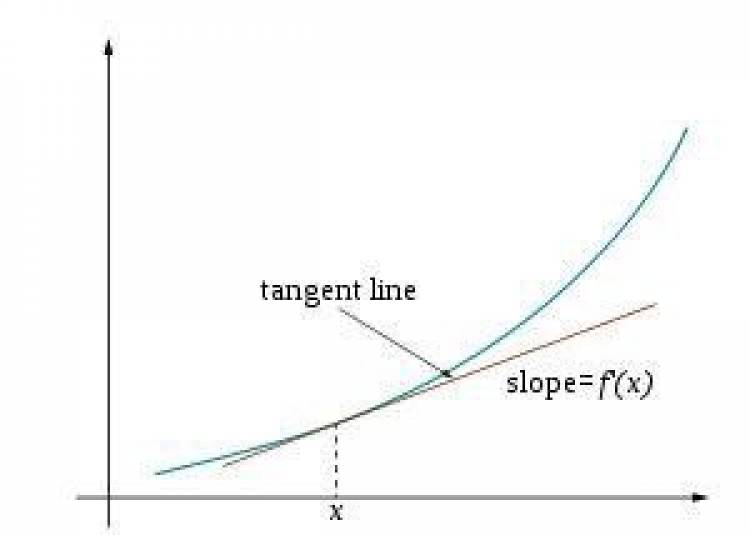2.อินทีกรัล แคลคูลัส (integral calculus) การคำนวณหาพื้นที่ที่ถูกปิดล้อมด้วยเส้นโค้ง

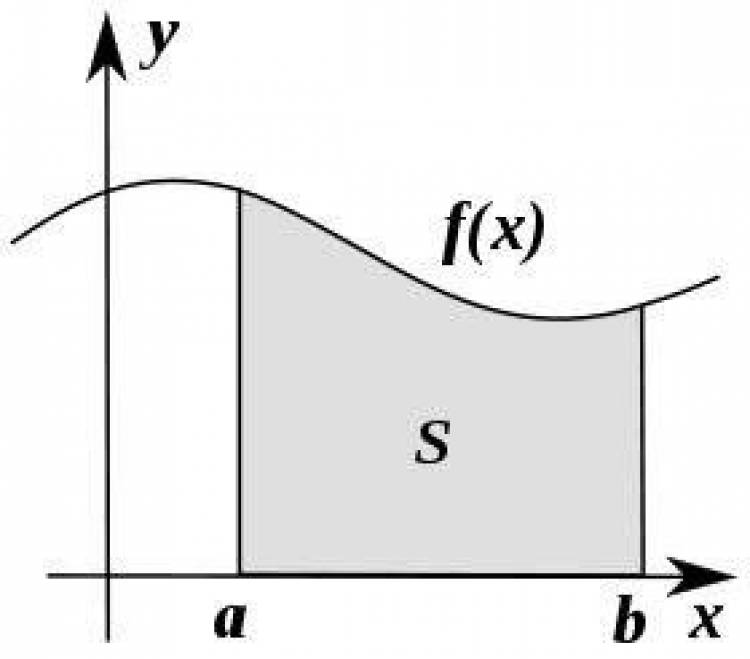
ทั้งสองอย่างนี้เป็นกระบวนการย้อนกลับของกันและกัน

และเชื่อมโยงกันด้วยทฤษฎีบทพื้นฐานของแคลคูลัส (Fundamental theorem of calculus)

กล่าวโดยสรุปได้ว่า มันเป็นเหมือนหน้าทั้งสองของเหรียญเดียวกันนั่นเอง

หัวใจอย่างหนึ่งที่ทำให้แคลคูลัสเกิดขึ้นได้ คือ การแบ่งสิ่งต่างๆออกเป็นส่วนที่เล็กจนเข้าใกล้ศูนย์

ลองนึกถึงตอนเราปล่อยหินจากยอดตึกให้ตกลงสู่พื้น แล้วหินตกกระทบพื้นภายในเวลา 4 วินาที

คำถามคือ หลังจากปล่อยหินไปได้ 3 วินาที หินมีความเร็วเท่าไหร่?

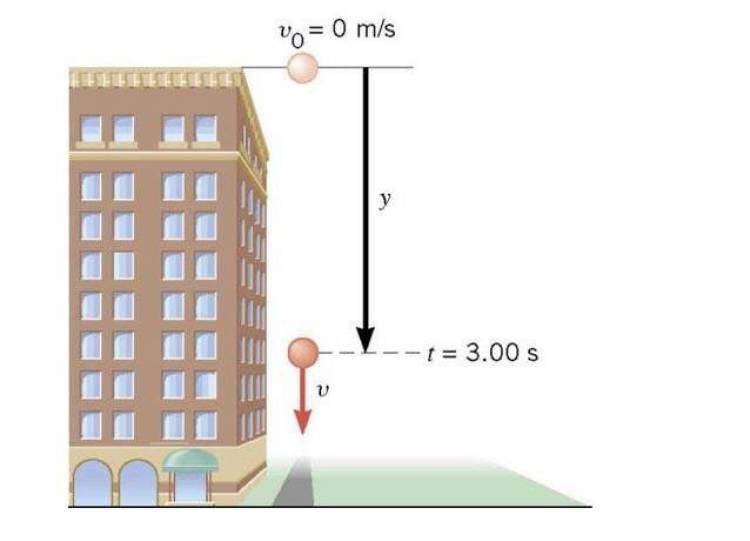
วิธีการหาคำตอบ คือ สังเกตว่าก่อน 3 วินาทีเล็กน้อยหินอยู่ตรงไหน และหลัง 3 วินาทีเล็กน้อยหินอยู่ตรงไหน

ตำแหน่งทั้งสองทำให้เราหาได้ว่าหินเคลื่อนที่ไปได้แค่ไหน แล้วจึงหารช่วงเวลานั้น

นั่นคือความเร็วเฉลี่ยในช่วง 3 วินาที

หากช่วงเวลานั้นเล็กมากจน"เข้าใกล้ศูนย์" เราจะได้ความเร็วที่ตำแหน่ง 3 วินาทีออกมา!

แม้จะฟังดูแปลก แต่เราก็ใช้มันในการหาความเร็วและปริมาณต่างๆที่เกี่ยวข้องกับการเปลี่ยนแปลงทั้งหมด

เพราะอัตราการเปลี่ยนแปลงคือความชัน

นอกจากนี้เรายังใช้การแบ่งซอยพื้นที่ออกเป็นส่วนเล็กๆในการหาพื้นที่ทั้งหมดที่เส้นโค้งปิดล้อมด้วย

กล่าวได้ว่าเมื่อมนุษย์เราเราสามารถหาความชัน และ หาพื้นที่ใต้กราฟได้ มนุษย์ก็มีอุปกรณ์ที่ช่วยในการวิเคราะห์ธรรมชาติของเส้นโค้งได้อย่างลึกซึ้งและสะดวก

ทำให้วิศวกรออกแบบโครงสร้างโค้งๆต่างๆได้

ทำให้นักเศรษฐศาสตร์วิเคราะห์แนวโน้มและปริมาณทางการเงินได้ (แต่จะทำนายถูกหรือไม่นั้นเป็นอีกเรื่อง)

ที่สำคัญคือ ทำให้นักฟิสิกส์ หาตำแหน่งและความเร็วของสิ่งที่ต้องการได้

นี่เป็นสาเหตุให้แคลคูลัสจึงเป็นกุญแจดอกแรก

ที่ใช้ในการทำความเข้าใจธรรมชาติของความเปลี่ยนแปลงที่อยู่ในวิชาต่างๆ

หากปราศจากซึ่งแคลคูลัส

เราคงจะ งงๆ กับเส้นโค้งต่างๆและวิเคราะห์อะไรได้อย่างยากลำบาก และถึงเราจะไม่ถึงกับเข้าใจแคลคูลัสอย่างลึกซึ้งถ่องแท้

อย่างน้อยๆขณะเรียนเราก็ควรเข้าใจหลักการพื้นฐานและการคำนวณพื้นฐานได้บ้าง

มาถึงตรงนี้เราควรขอบคุณผู้ที่สร้างสรรค์วิชาแคลคูลัสขึ้นมา ราวๆ 325 ปีก่อน

แต่การถือกำเนิดของแคลคูลัสนั้นไม่ธรรมดาเพราะมันเกิดขึ้นจากมันสมองของอัจฉริยะสองคนในยุคนั้น

คนแรกเป็น ชาวอังกฤษ ผู้มีนามว่า ไอแซค นิวตัน

อีกคน เป็นชาวเยอรมัน ชื่อ ก็อทฟรีท ไลบ์นิทซ์

ทั้งสองอยู่ในยุคเดียวกันและมีมันสมองระดับอัจฉริยะ

อีกทั้งแคลคูลัสยังเป็นหนึ่งในผลงานแห่งยุคสมัย จึงไม่น่าแปลกใจที่ทั้งสองจะทุ่มเถียงกันว่าใครเป็นผู้คิดค้นแคลคูลัส จนกลายเป็นสงครามโลกคณิตศาสตร์ซึ่งจะเล่าให้ฟังครั้งหน้าครับ

cr. อาจวรงค์ จันทมาศ  https://www.blockdit.com/articles/5bf640490738e63c86565d83